Correction of Gravity Measurements: Bouguer Correction Latitude Correction Terrain Corrections Free Air Correction

Correction of Gravity Measurements:

If the interior of the Earth were uniform, the value of gravity on the International Reference Ellipsoid would vary with latitude according to the normal gravity formula. This provides us with a reference value for gravity measurements. In practice, it is not possible to measure gravity on the ellipsoid: the elevation of a measurement station may be hundreds of meters above or below the ellipsoid.

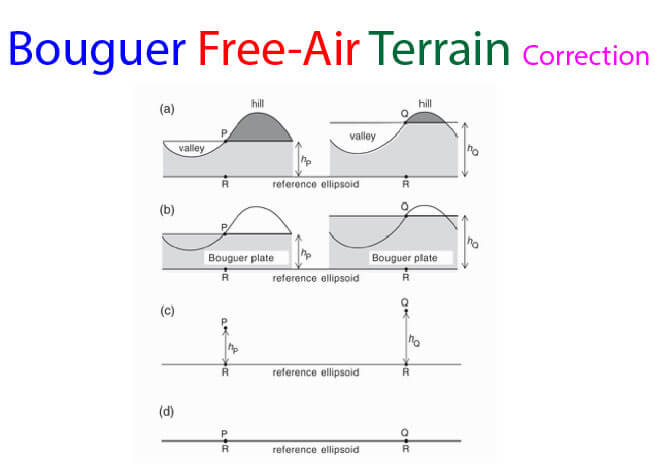
Moreover, the gravity station may be surrounded by mountains and valleys that perturb the measurement. For example, let P and Q represent gravity stations at different elevations in hilly terrain.

The theoretical value of gravity is computed at point R on the reference ellipsoid below P and Q. Thus, we must correct the measured gravity before it can be compared with the reference value.

The hill to the right of stations P and Q has a center of mass that lies higher than the measurement elevation. “The gravimeter measures gravity in the vertical direction, along the local plumb line. The mass of the hilltop above P attracts the gravimeter and causes an acceleration with a vertically upward component at P. The measured gravity is reduced by the presence of the hill-top; to compensate for this a terrain (or topographic) correction is calculated and added to the measured gravity. A similar effect is observed at Q, but the hilltop above Q is smaller and the corresponding terrain correction is smaller.

These corrections effectively level the topography to the same elevation as the gravity station. The presence of a valley next to each measurement station also requires terrain correction. In this case, imagine that we could fill the valley up to the level of each station with the rock of the same density ρ as under P and Q. The downward attraction on the gravimeter would be increased, so the terrain correction for a valley must also be added to the measured gravity, just as for a hill. Removing the effects of the topography around a gravity station requires making positive terrain corrections (∆gT) for both hills and valleys.

After effectively leveling the topography with the terrain correction, the rock between the gravity station and the reference ellipsoid is modeled as a uniform layer with density ρ. The gravitational acceleration of this rock mass is included in the measured gravity and must be removed before we can compare it with the theoretical gravity. The layer is taken to be a flat disk or plate of thickness hP or hQ under each station; it is called the Bouguer plate.

Its gravitational acceleration can be computed for known thickness and density ρ, and gives a Bouguer plate correction (∆gBP) that must be subtracted from the measured gravity if the gravity station is above sea level.”

Note that if the gravity station is below sea level, we have to fill the space above it up to sea level with the rock of density ρ; this requires increasing the measured gravity correspondingly. The Bouguer plate correction (∆gBP) is negative if the station is above sea level but positive if it is below sea level. Its size depends on the density of the local rocks but typically amounts to about 0.1 mGal m–1.

Finally, we must compensate the measured gravity for the elevation hP or hQ of the gravity station above the ellipsoid. The main part of gravity is due to gravitational attraction, which decreases proportionately to the inverse square of the distance from the center of the Earth. The gravity measured at P or Q is smaller than it would be if measured on the ellipsoid at R. A free-air correction (∆GFA) for the elevation of the station must be added to the measured gravity.

This correction ignores the effects of material between the measurement and reference levels, as this is taken care of in ∆GBP. Note that, if the gravity station were below sea level, the gravitational part of the measured gravity would be too large by comparison with the reference ellipsoid; we would need to subtract ∆GFA in this case. The free-air correction is positive if the station is above sea level but negative if it is below sea level (as might be the case in Death Valley or beside the Dead Sea). It amounts to about 0.3 mGal m–1.

The free-air correction is always in the opposite sense of the Bouguer plate correction. For convenience, the two are often combined in a single elevation correction, which amounts to about 0.2 mGal m–1. This must be added for gravity stations above sea level and subtracted if gravity is measured below sea level. In addition, a tidal correction (∆gtide) must be made and, if gravity is measured in a moving vehicle, the Eötvös correction is also necessary.

After correction, the measured gravity can be compared with the theoretical gravity on the ellipsoid. Note that the above procedure reduces the measured gravity to the surface of the ellipsoid. In principle, it is equally valid to correct the theoretical gravity from the ellipsoid upward to the level where the measurement was made. This method is preferred in more advanced types of analysis of gravity anomalies where the possibility of an anomalous mass between the ellipsoid and ground surface must be taken into account.”

Time-Dependent Corrections:

If a gravimeter is set up at a given place and monitored continuously, the readings are found to vary smoothly with time. The changes may amount to several hundredths of a mGal and thus may exceed the gravity anomaly that is to be measured. In part, the changes are characteristic of the instrument; the remainder is caused by the tides. Transient changes are unrelated to the gravitational attraction of any local mass anomaly, therefore gravity measurements must be corrected for them.

“The instrumental drift is partly due to thermally induced changes in the elastic properties of the gravimeter spring, which are minimized by housing the critical elements in an evacuated chamber. In addition, the elastic properties of the spring are not perfect but creep slowly with time. The effect is small in modern gravimeters and can be compensated by making a drift correction. This is obtained by repeated occupation of some measurement stations at intervals during the day. Gravity readings at other stations are adjusted by comparison with the drift curve. In order to make this correction the time of each measurement must be noted.

During the course of a day, while measurements are being made at a particular location, the gravimeter is subject to tidal attractions, including vertical displacement due to the bodily Earth tides. The theory of the tides is known very well and their time-dependent effects on gravity can be computed precisely for any place on Earth at any particular time. Consequently, the tidal correction also requires that the time of each measurement be carefully noted.

Latitude Correction

The correction is maximum at latitude 45°. Because gravity increases toward the poles, the correction for stations closer to the pole than the base station must be subtracted from the measured gravity, while for stations further from the pole, the correction must be added.

Terrain Corrections

The terrain correction (∆gT) for a hill adjacent to a gravity station is computed by dividing the hill into a number of vertical prisms. The contribution of each vertical element to the vertical acceleration at the point of observation P is calculated by assuming cylindrical symmetry about P. The height of the prism is h, its inner and outer radii are r1 and r2, respectively, the angle subtended at P is ϕ0, and the density of the hill is ρ.

The traditional method of making terrain corrections was both time-consuming and tedious. The computational principle is followed in modern analyses, which use databases of digitized topography instead of simple maps. As a result, terrain corrections can now be made rapidly and easily by computers. For topography that is more than 22 km from the measurement station, the effect of the curvature of the Earth is also taken into account.

Bouguer Plate Correction

“The Bouguer plate correction (∆gBP) compensates for the effect of a layer of rock whose thickness corresponds to the elevation difference between the measurement and reference levels.

An additional consideration is necessary for marine gravity surveys. ∆gBP requires uniform density below the surface of the reference ellipsoid. To compute ∆gBP over an oceanic region we must in effect replace the seawater with the rock of density ρ. However, the measured gravity contains a component due to the attraction of the seawater (density 1030 kg m–3) in the ocean basin.  When a shipboard gravity survey is made over a large, deep lake, a similar allowance must be made for the depth of water in the lake using an assumed density of (ρ– 1000) kg m–3.

Free-Air Correction

The free-air correction (∆gFA) has a rather colorful, but slightly misleading title, giving the impression that the measurement station is floating in the air above the ellipsoid. The density of air at standard temperature and pressure is around 1.3 kg m–3 and a mass of air between the observation and reference levels would cause a detectable gravity effect of about 50 µGal at an elevation of 1000 m.

In fact, the free-air correction pays no attention to the density of the material between the measurement elevation and the ellipsoid. It is a straightforward correction for the decrease of gravitational acceleration with distance from the center of the Earth:

On substituting the Earth’s radius (6371 km) for r and the mean value of gravity (981,000 mGal) for g, the value of ∆gFA is found to be 0.3086 mGal m–1.

Combined Elevation Correction

The free-air and Bouguer plate corrections are often combined into a single elevation correction, which is (0.3086 – (4.19ρ × 10–5)) mGal m–1. Substituting a typical density for crustal rocks, usually taken to be 2670 kg m–3, gives a combined elevation correction of 0.197 mGal m–1. This must be added to the measured gravity if the gravity station is above the ellipsoid and subtracted if it is below.

The high sensitivity of modern gravimeters allows an achievable accuracy of 0.01–0.02 mGal in modern gravity surveys. To achieve this accuracy the corrections for the variations of gravity with latitude and elevation must be made very exactly. This requires that the precise coordinates of a gravity station must be determined by accurate geodetic surveying. The necessary precision of horizontal positioning is indicated by the latitude correction.

This is maximum at 45° latitude, where, in order to achieve a survey accuracy of ± 0.01 mGal, the north–south positions of gravity stations must be known to about ± 10 m. The requisite precision in vertical positioning is indicated by the combined elevation correction of 0.2 mGal m–1. To achieve a survey accuracy of ± 0.01 mGal the elevation of the gravimeter above the reference ellipsoid must be known to about ± 5 cm.

The elevation of a site above the ellipsoid is not the same as its altitude above mean sea level, which is equated with the geoid and not with the ellipsoid. Geoid undulations can amount to tens of meters relative to the ellipsoid (Section 3.4.5.1). However, they are long-wavelength features.

Within a local survey, the height difference between geoid and ellipsoid may not vary much, and the gravity differences from the selected base station are unlikely to be strongly affected. In surveys at a regional scale, the discrepancies due to geoid undulations may be more serious. In the event that geoid undulations are large enough to affect a survey, the station altitudes must be corrected to true elevations above the ellipsoid.

Reference Book: William Lowrie. “Fundamentals of Geophysics”. Apple Books.