Gravity Anomaly: A difference between the locally observed and the theoretically calculated
value of gravity that reflects local variations in density of underlying rocks and is often
helpful in geophysical prospecting.
Gravity anomalies are the difference between the observed acceleration of earths gravity and
the values predicted from some model of how the gravity would be predicted to appear. The
gravity anomalies at a location on the earths surface is the difference between the observed
value of gravity and the value predicted by a theoretical model.
The three most commonly used gravity anomalies are the
1.Free-air or faye gravity anomaly
2.the Bouger gravity anomaly
3. the isostatic gravity anomaly.
Other varieties of gravity anomalies have been propoesd, for example the Rudzki inversion and helmert condensation gravity anomalies but these are seldom used.
1.Free- air anomaly:
In geophysics free- air gravity anomaly often called the free-air
anomaly.Free –air anomaly is the measured gravity anomaly after a free-air correction is
applied to account for the elevation at which a measurement is made.
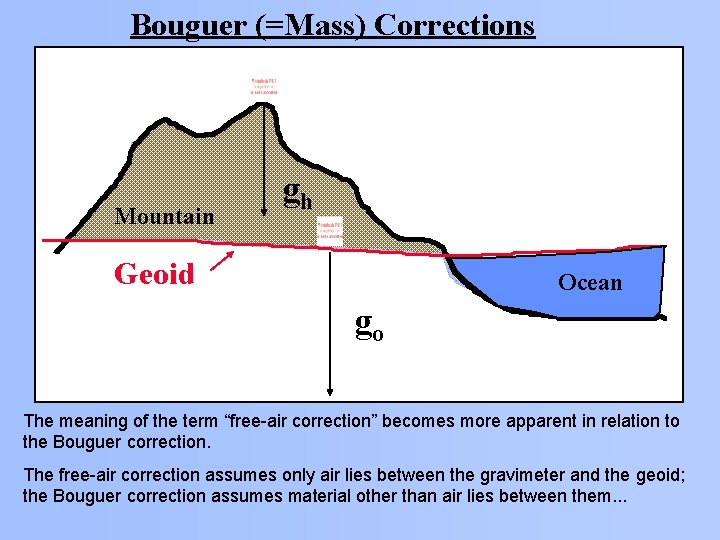
2. Bouguer anomaly:
The Bouguer anomaly is the difference between the expected
value of gravity at a given location(taking into account factors such as
latitude, longitude, altitude and the rotation of the earth) and its actual value. Bouguer
anomalies can be measured in several ways depending whether the density and shape of the
terrain between the measuring point and sea level is calculated, estimated or ignored.
3.Isostatic gravity anomaly:
Isostatic gravity anomalies are alleged to provide a measure of
the earths gravity field free from the gravitational attractions of the topography and its isostatic
compensation. Most commonly represented by a variation in the depth of a compensating
density contrast for example the moho.
Gravity anomalies are often due to unusual concentrations of mass in a region. For example, the presence of mountain ranges will usually cause the gravitational force to be more than it would be on a featureless planet.-positive anomaly. A positive anomaly is reading that exceeds the average magnetic
field strength and is usually related to more strongly magnetic rocks,such as mafic rocks or
magnetic-bearing rocks, underneath the magnetometer.A negative magnetic anomaly is a
reading that is lower than the average magnetic field. Negative anomalies are
interested to mean that the segments of the lithosphere( that is the crust and upper mantle
comprising the rigid, outermost shell of the earth) that underlie trenches are being forced
down against buoyant isostatic forces.
In geodesy and geophysics, the bouguer anomaly (named after pierre Bouguer) is a
anomaly, corrected for a hight at which it is measured and the attraction of terrain.The heighet
correction alone gives a free-air gravity anomaly. Otherwise the bouguer reduction does not
work properly.
